Widerstandsmomente & Trägheitsmomente
Ihr professioneller Online-Kalkulator für Querschnittsberechnungen im Maschinenbau
Interaktiver Satz von Steiner - Kalkulator
Erstellen Sie Ihren eigenen Querschnitt aus Rechtecken, Kreisen oder Rohren.
| Vorlagen: | |||||
| Nr. | Breite b / Ø (mm) | Höhe h / Øi (mm) | X (mm) | Y (mm) | |
|---|---|---|---|---|---|
|
Modus:
|
|||||
Belastungen / Spannungen
* Spannungen werden in N/mm² (MPa) berechnet. Torsion für offene Profile genähert.
Alle Angaben ohne Gewähr. Für die Richtigkeit der Ergebnisse wird keine Haftung übernommen.
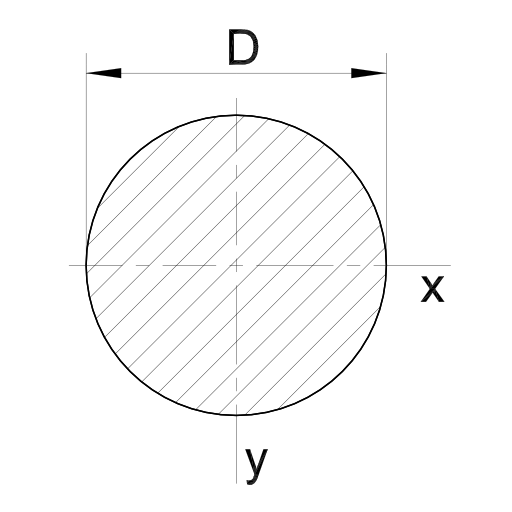
Kreisquerschnitt
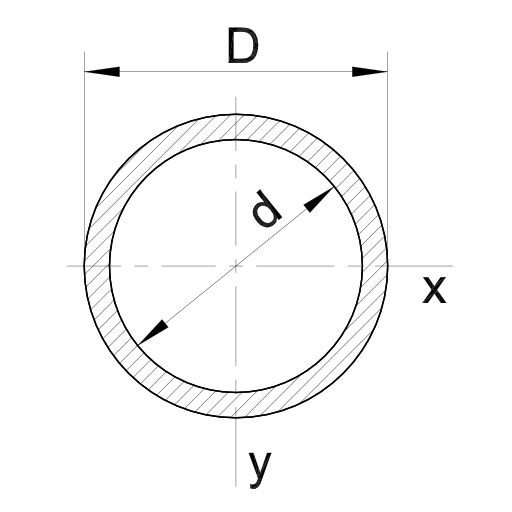
Kreisring / Rohr
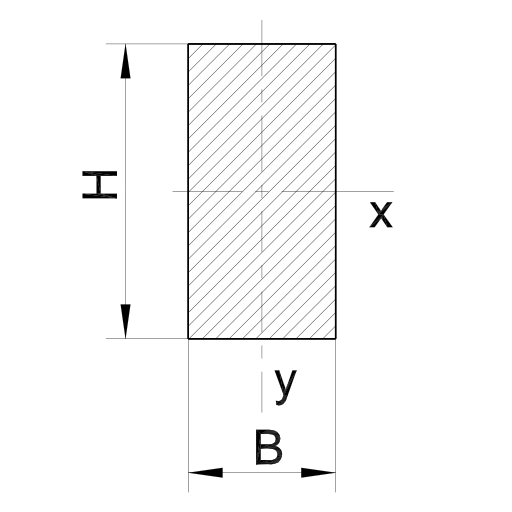
Rechteck-Profil
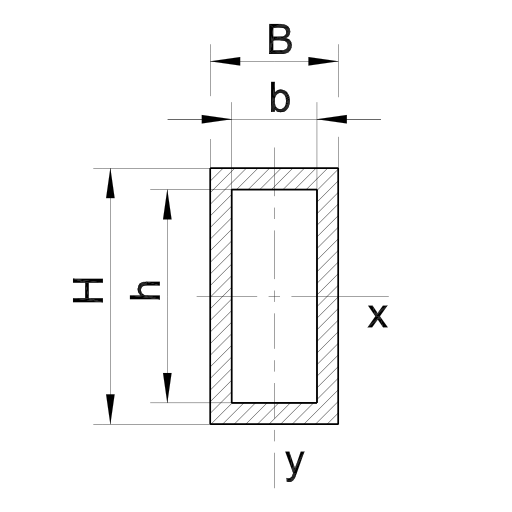
Rechteck-Hohlprofil
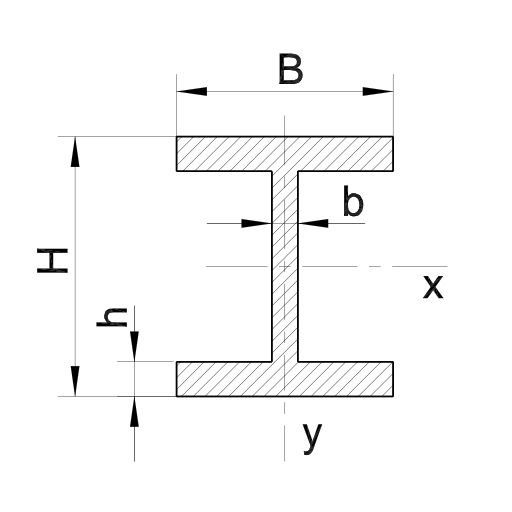
I- / H-Profil
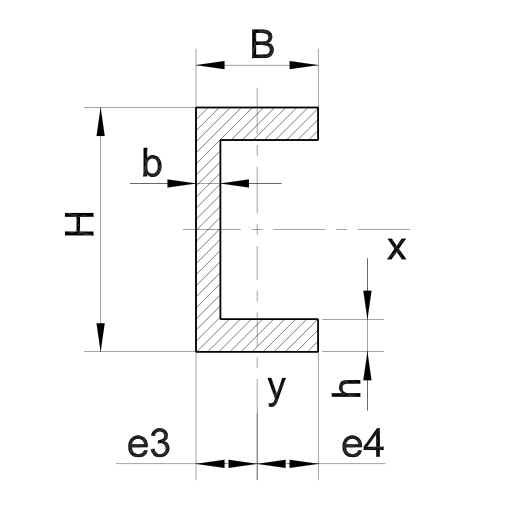
U- / C-Profil
Weitere Engineering Leistungen
Sie haben spezielle Anforderungen oder benötigen Unterstützung bei komplexen Berechnungen? Vertrauen Sie auf unsere über 20-jährige Erfahrung im Sondermaschinenbau und Engineering. Wir begleiten Sie von der Idee bis zur fertigen Lösung.
Zu unseren Dienstleistungen